计算机图形学中的四元数
四元数与欧拉角
以下内容主要是参考了Krasjet关于四元数的介绍《四元数与三维旋转》:“点这里阅读《四元数与三维旋转》”
会记录一些阅读过程中遇到的结论性内容,系统学习主要还是参考原文档为主
复数
1.3 复数相乘与2D旋转
与复数 \(z=a+bi\) 相乘代表着\(\begin{bmatrix}a & -b \\b & a \end{bmatrix}\) 矩阵所作出的变换,将矩阵中的每一个元素都除以模长,可以得到以下变换:
\[ \begin{bmatrix}a & -b \\b & a \end{bmatrix} = \sqrt{a^2+b^2}*\begin{bmatrix}\frac{a}{\sqrt{a^2+b^2}}&\frac{-b}{\sqrt{a^2+b^2}}\\\frac{b}{\sqrt{a^2+b^2}}&\frac{a}{\sqrt{a^2+b^2}}\end{bmatrix} \]
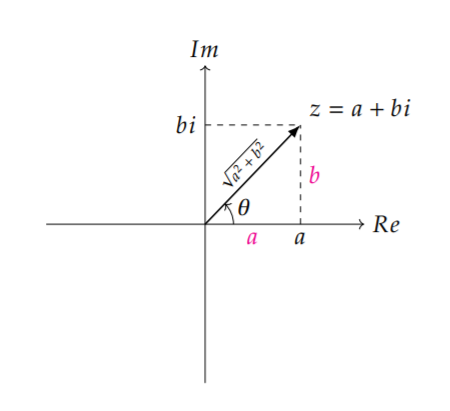
从复平面观察可以得到,\(\|z\|=\sqrt{a^2+b^2}\) 且有 \(\theta=\arctan(\frac{b}{a})\) ,原本的矩阵转换为了两个变换矩阵的复合,其中左边的\(\begin{bmatrix}\|z\|&0\\0&\|z\|\end{bmatrix}\)是缩放矩阵,而右边的\(\begin{bmatrix}\cos( \theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix}\)则是2D旋转矩阵。
1.4 旋转的复合
\[ \begin{aligned}z_{net}&=(\cos(\theta)+i\sin(\theta))(\cos(\phi)+i\sin(\phi))\\&=\cos(\theta+\phi)+i\sin(\theta+\phi)\end{aligned} \]
对两个2D旋转进行复合时,所得的变换 \(z_{net}\) 仍是一个旋转,而且与施加的次序无关。这个等效变换的旋转角是两个旋转角之和。
2 三维空间中的旋转
轴角式(Axis-angle) 旋转:给定旋转的转轴向量\(\vec{u}=(x,y,z)^T\)以及旋转的角度\(\theta\),但实际在三维空间中表示方向只需要两个自由度(或者说两个变量),即与两个坐标轴的夹角,转轴向量可以除以模长转换为特定方向上的单位向量。
2.1 旋转的分解
首先将要旋转的向量在垂直和平行于转轴的方向上进行分解,有\(\vec{v}=\vec{v_\parallel}+\vec{v_\perp}\) ,分别进行旋转后再相加就能得到旋转后的结果。
根据正交投影公式,可以得出
\[ \begin{aligned}\vec{v_\parallel}&=proj_{\vec{u}}(\vec{v})\\&=\frac{\vec{u}\cdot\vec{v}}{\vec{u}\cdot\vec{u}}\vec{u}\\&=(\vec{u}\cdot\vec{v})\vec{u}\end{aligned} \]
又由于\(\vec{v}=\vec{v_\|}+\vec{v_\perp}\),可以得到垂直于转轴方向有
\[ \begin{aligned}\vec{v_{\perp}}&=\vec{v}-\vec{v_{\parallel}}\\&=\vec{v}-(\vec{u}\cdot\vec{v})\vec{u}\end{aligned} \]
2.3 垂直分量的旋转
在与\(\vec{u}\)垂直平面上的分量旋转角度\(\theta\),可对结果进行下述表示,先构造一个正交于转轴向量和\(\vec{v_{\perp}}\)的向量\(\vec{w}\):
\[ \vec{w}=\vec{u}\times\vec{v_\perp} \]
可以得到正交于旋转轴\(\vec{u}\)的分量\(\vec{v_\perp}\),旋转角度\(\theta\)后得到的\(\vec{v_\perp^\prime}\):
\[ \begin{aligned}\vec{v_\perp^\prime}&=\cos{\theta}\vec{v_\perp}+\sin{\theta}\vec{w}\\&=\cos{\theta}\vec{v_\perp}+\sin{\theta}(\vec{u}\times\vec{v_\perp})\end{aligned} \]
2.4 \(\vec{v}\)的旋转
根据上述公式可以得到以下推导,得到3D旋转公式,也称Rodrigues’ Rotation Formula:
\[ \begin{equation}\begin{aligned}\vec{v^\prime}&=\vec{v^\prime_\parallel}+\vec{v_\perp^\prime}\\&=\vec{v_\parallel}+\cos{\theta}\vec{v_\perp}+\sin{\theta}(\vec{u}\times\vec{v_\perp})\\&=(\vec{u}\cdot\vec{v})\vec{u}+\cos{\theta}(\vec{v}-(\vec{u}\cdot\vec{v})\vec{u})+\sin{\theta}(\vec{u}\times\vec{v})\\&=\cos{\theta}\vec{v}+(1-\cos{\theta})(\vec{u}\cdot\vec{v})\vec{u}+\sin{\theta}(\vec{u}\times\vec{v})\end{aligned}\end{equation} \]
其中第二步包含以下推导(叉乘遵守分配律)
\[ \begin{equation}\begin{aligned}\vec{u}\times\vec{v_\perp}&=\vec{u}\times(\vec{v}-\vec{v_\parallel})\\&=\vec{u}\times\vec{v}-\vec{u}\times\vec{v_\parallel}(\vec{u}平行于\vec{v_\parallel},结果为0)\\&=\vec{u}\times\vec{v}\end{aligned}\end{equation} \]
四元数
所有四元数\(q\in\mathbb{H}\)都可以表现成下述形式,有时四元数也写作w,x,y,z的形式,w是常数项,x,y,z分别是i,j,k维度上的系数(记住w是常数项就行)
\[ \begin{equation}\begin{aligned}q=a+bi+cj+dk(a,b,c,d\in\mathbb{R})\end{aligned}\end{equation} \]
其中有
\[ \begin{equation}i^2=j^2=k^2=ijk=-1\end{equation} \]
3.1 标量乘法 & 四元数乘法
四元数与标量的乘法遵守交换律,但四元数之间的乘法比较特殊不遵守交换律,有左乘与右乘的区别,一般情况下左乘结果不等于右乘结果。举例对\(q_1=a+bi+cj+dk\)与\(q_2=e+fi+gj+hk\)之间的乘法有:
\[ \begin{equation}q_1q_2=\begin{bmatrix}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{bmatrix}\begin{bmatrix}e\\f\\g\\h\end{bmatrix}\end{equation} \]
进行\(q_1\)右乘\(q_2\)有以下
\[ \begin{equation}q_2q_1=\begin{bmatrix}a&-b&-c&-d\\b&a&d&-c\\c&-d&a&b\\d&c&-b&a\end{bmatrix}\begin{bmatrix}e\\f\\g\\h\end{bmatrix}\end{equation} \]
3.1.6 Graßmann积
对以上\(q_1\)以及\(q_2\)有两者的乘积
\[ \begin{equation}\begin{aligned}q_1q_2=&(ae-(bf+cg+dh))+\\&(be+af+ch-dg)i+\\&(ce+ag+df-bh)j+\\&(de+ah+bg-cf)k\end{aligned}\end{equation} \]
若给出以\(\vec{i}、\vec{j}、\vec{k}\)为基的向量\(\vec{v}=\begin{bmatrix}b\\c\\d\end{bmatrix}\)以及\(\vec{u}=\begin{bmatrix}f\\g\\h\end{bmatrix}\),有以下
\[ \begin{equation}\begin{aligned}\vec{v}\cdot\vec{u}&=bf+cg+dh\\\vec{v}\times\vec{u}&=\left|\begin{matrix}\vec{i}&\vec{j}&\vec{k}\\b&c&d\\f&g&h\end{matrix}\right|\\&=(ch-dg)\vec{i}-(bh-df)\vec{j}+(bg-cf)\vec{k}\end{aligned}\end{equation} \]
最后可以得到Graßmann积结果,有对任意四元数\(q_1=\begin{bmatrix}s,\vec{v}\end{bmatrix}, q_2=\begin{bmatrix}t,\vec{u}\end{bmatrix}\)可以得到结果:
\[ \begin{equation}q_1q_2=\begin{bmatrix}st-\vec{v}\cdot\vec{u}, s\vec{u}+t\vec{v}+\vec{v}\times\vec{u}\end{bmatrix}\end{equation} \]
需要留意这里的到的结果是一个四元数,前者是标量,后者是一个以\(\vec{i}、\vec{j}、\vec{k}\)为基的三维向量
3.1.7 纯四元数
纯四元数是仅有虚部的四元数,因为纯四元数仅由虚部的3D向量决定,所以可以将任意的3D向量转换为纯四元数。对3D向量\(\vec{v}\),有对应的纯四元数:
\[ \begin{equation}v=\begin{bmatrix}0, \vec{v}\end{bmatrix}\end{equation} \]
可以思考一下对于纯四元数来说Graßmann积(14)会得到什么结果
3.1.8 逆与共轭
对四元数\(q\),它的逆为\(q^{-1}\),相乘积为1,这里注意复习下四元数不遵守交换律
同样对四元数\(q = a+bi+cj+dk\) 有共轭为 \(q^* = a-bi-cj-dk\),四元数\(q\)与共轭\(q^*\)相乘得到结果为四元数模长的平方\({\|q\|}^2\),同时这个特殊的运算是遵守交换律的
最后,根据逆的定义可以推导得到一种寻找四元数的逆的方式,即:
\[ \begin{equation}q^{-1}=\frac{q^*}{\|q\|^2}\end{equation} \]
3.2 四元数与3D旋转
接下来的内容就是将先前推导过的3D旋转公式(14),用四元数的计算和纯四元数的方式进行表达,这里开始搬运的内容会减少,请主要以阅读原pdf为主。
对旋转向量\(\vec{v}\)在垂直方向上的分量旋转\(\theta\)后的结果\(\vec{v_\perp^\prime}\),替换为纯四元数的形式有:
\[ \begin{equation}\begin{aligned}v_\perp^\prime&=\cos{\theta}v_\perp+\sin{\theta}(uv_\perp)\\&=(\cos{\theta}+\sin{\theta}u)v_\perp\\&=qv_\perp\\q&=\begin{bmatrix}\cos{\theta},\sin{\theta}\vec{u}\end{bmatrix}\end{aligned}\end{equation} \]
这里的\(q\)是一个单位四元数,根据(16)可以得到\(q^{-1}=q^\star\)
对平行于旋转轴的\(\vec{v_\parallel}\),旋转后的保持不变,四元数表达形式:\(v_\parallel^\prime=v_\parallel\)
\[ \begin{equation}\begin{aligned}v^\prime&=v_\parallel^\prime+v_\perp^\prime\\&=v_\parallel+qv_\perp\\&=1\cdot{v_\parallel}+qv_\perp\\&=pp^{-1}v_\parallel+ppv_\perp(令p^2=q,p=[cos(\frac{1}{2}\theta),sin(\frac{1}{2}\theta)\vec{u})])\\&=p{v_\parallel}p^*+p{v_\perp}p^*\\&=p(v_\parallel+v_\perp)p^*\\&=pvp^*\end{aligned}\end{equation} \]
其中第四步涉及到一个引理证明,第五涉及到两个引理证明,这里就不进行搬运了。
最后我们可以得到四元数型,一般情况的3D旋转公式,对任意向量\(\vec{v}\)沿以单位向量定义的旋转轴\(\vec{u}\)旋转\(\theta\)度后得到的\(\vec{v^\prime}\)可以通过四元数乘法得到,令\(v=\begin{bmatrix}0,\vec{v}\end{bmatrix}, q=\begin{bmatrix}\cos({\frac{1}{2}\theta}),\sin({\frac{1}{2}\theta})\vec{u}\end{bmatrix}\),有
\[ \begin{equation}v^\prime=qvq^*=qvq^{-1}\end{equation} \]
3.3 3D旋转的矩阵形式
对左乘一个四元数\(q=a+bi+cj+dk\)等同于下面这个矩阵
\[ \begin{equation}L(q)=\begin{bmatrix}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\\\end{bmatrix}\end{equation} \]
同样的,右乘q等同于这个矩阵
\[ \begin{equation}R(q)=\begin{bmatrix}a&-b&-c&-d\\b&a&d&-c\\c&-d&a&b\\d&c&-b&a\\\end{bmatrix}\end{equation} \]
对先前的\(q=\begin{bmatrix}\cos({\frac{1}{2}\theta}),\sin({\frac{1}{2}\theta})\vec{u}\end{bmatrix}\),可以转换成\(a=\cos(\frac{1}{2}\theta), b=\sin(\frac{1}{2}\theta)u_x,c=\sin(\frac{1}{2}\theta)u_y,d=\sin(\frac{1}{2}\theta)u_z, q=a+bi+cj+dk\),我们就能得到
\[ \begin{equation}qvq^*=\begin{bmatrix}1&0&0&0\\0&1-c^2-2d^2&2bc-2ad&2ac+abd\\0&2bx+2ad&1-2b^2-2d^2&2cd-2ab\\0&2bd-2ac&2ab+2cd&1-2b^2-2c^2\end{bmatrix}v\end{equation} \]
注意了,这里的\(v\)是纯四元数,等式左侧也是四元数的形式下的3D旋转
由于我们知道\(v=\begin{bmatrix}0,\vec{v}\end{bmatrix}\),所以上述矩阵的最外圈不会进行任何变换,可以将它压缩成3x3的矩阵,3D旋转的矩阵形式不如四元数形式简单,且占用更多空间,但是预计算好的矩阵对于大批量的变换是更有效率的。
\[ \begin{equation}\vec{v^\prime}=\begin{bmatrix}1-c^2-2d^2&2bc-2ad&2ac+abd\\2bx+2ad&1-2b^2-2d^2&2cd-2ab\\2bd-2ac&2ab+2cd&1-2b^2-2c^2\end{bmatrix}\vec{v}\end{equation} \]
TODO 你可能还会需要
四元数欧拉角之间的变换:http://zhaoxuhui.top/blog/2018/03/13/RelationBetweenQ4&R&Euler.html#5欧拉角转四元素
让你快速变换的网站工具:
万向节死锁
包含了万向节死锁的部分问题,以Unity为例的回答
为什么Unity3d旋转默认采用了有万向节死锁的欧拉角,而不用四元数?
个人向的梳理总结:
万向节死锁(Gimbal Lock),是指在将一个旋转拆分成物体自身三个正交坐标轴,并按照固定次序旋转的情况下,存在特殊情况使得其中的两次旋转变换实际上变换的是同一个轴(外部轴/世界坐标轴)。
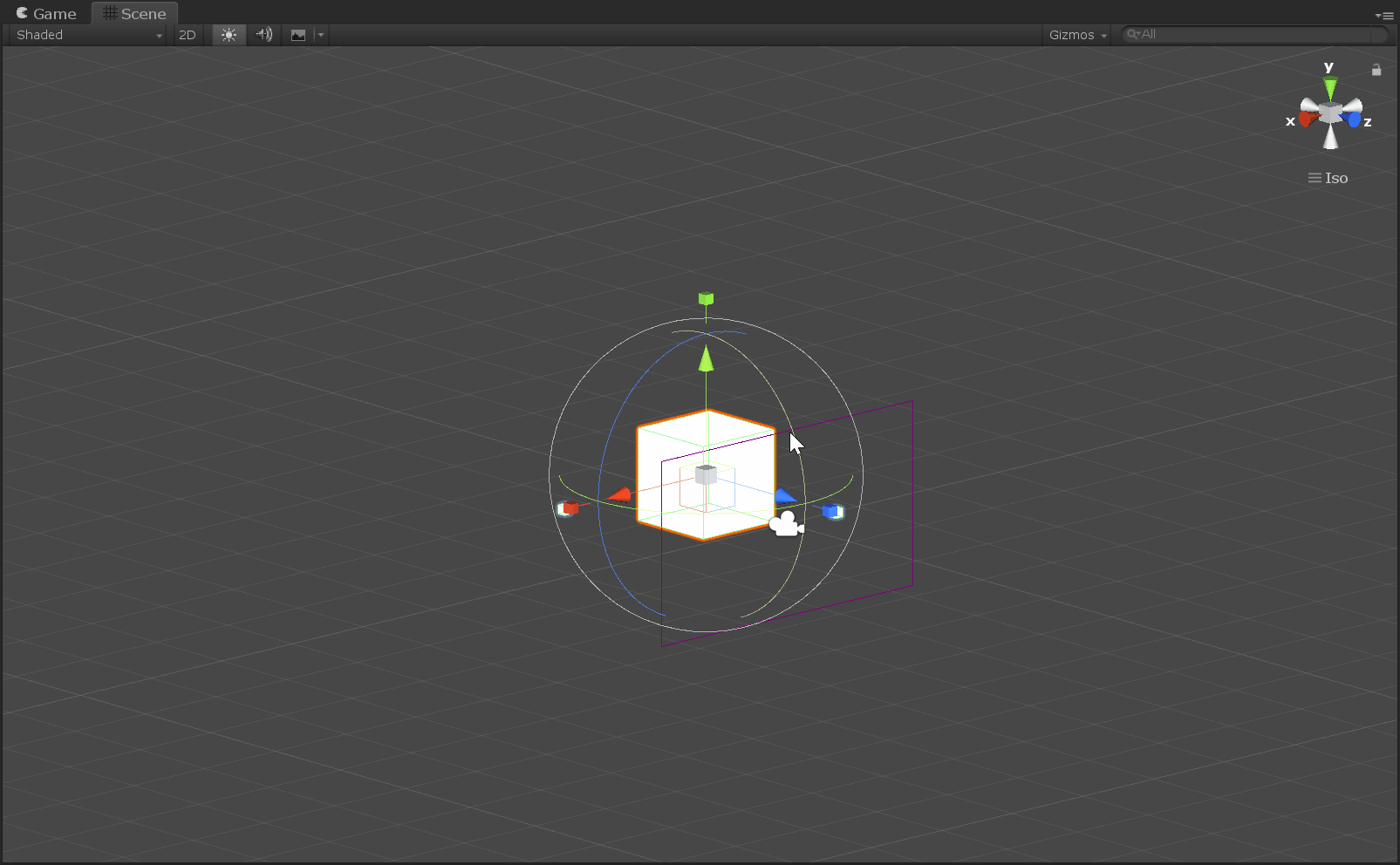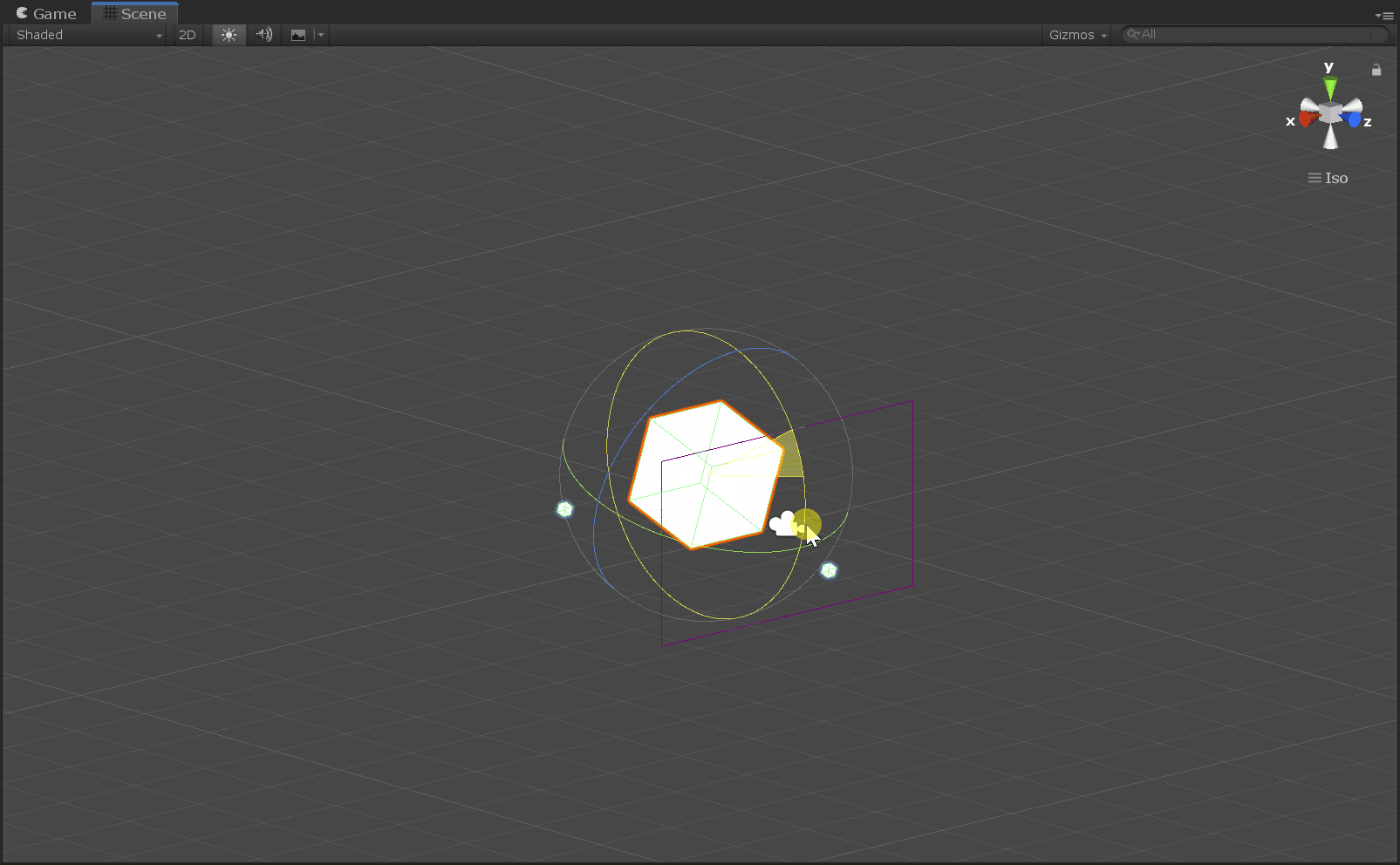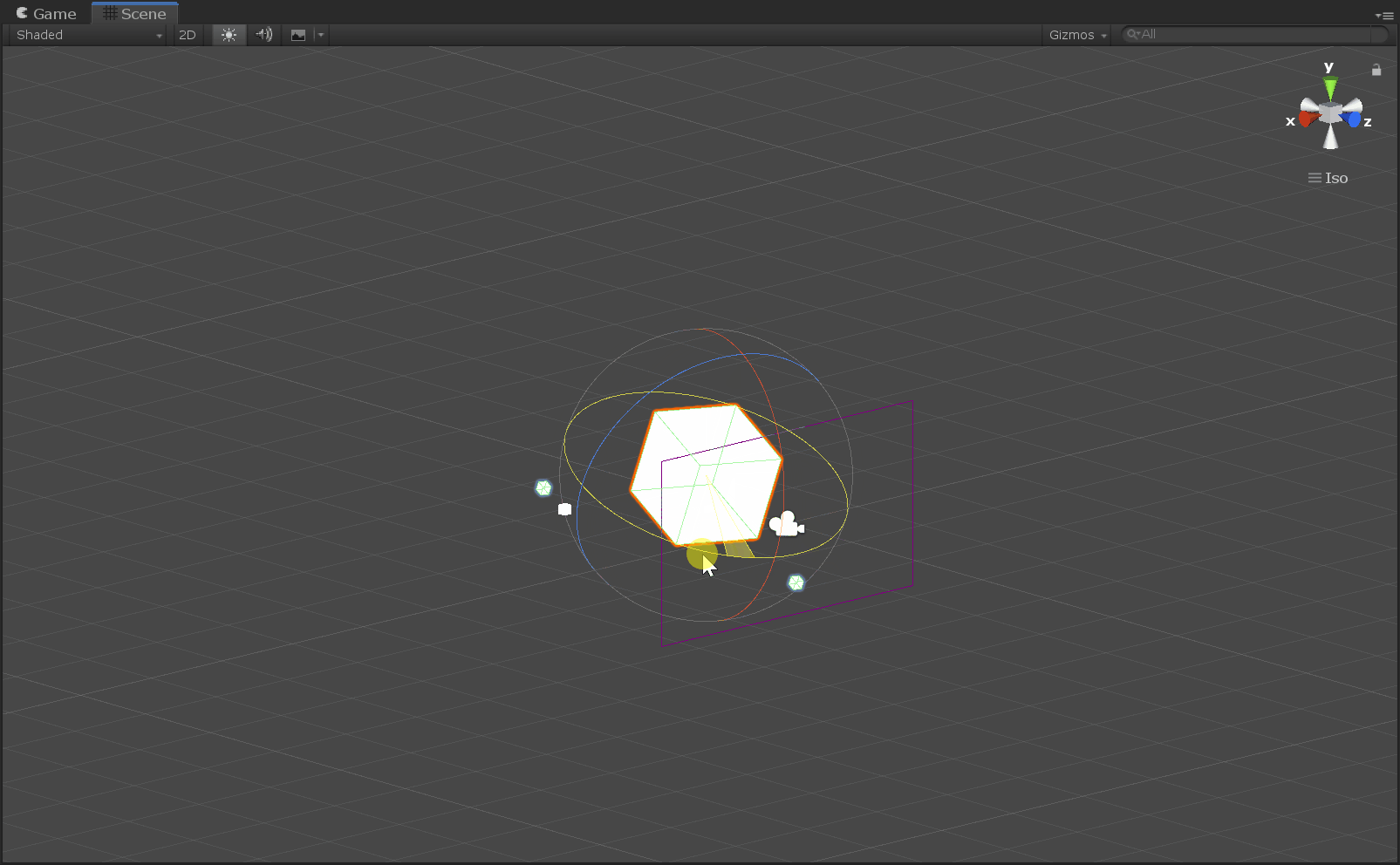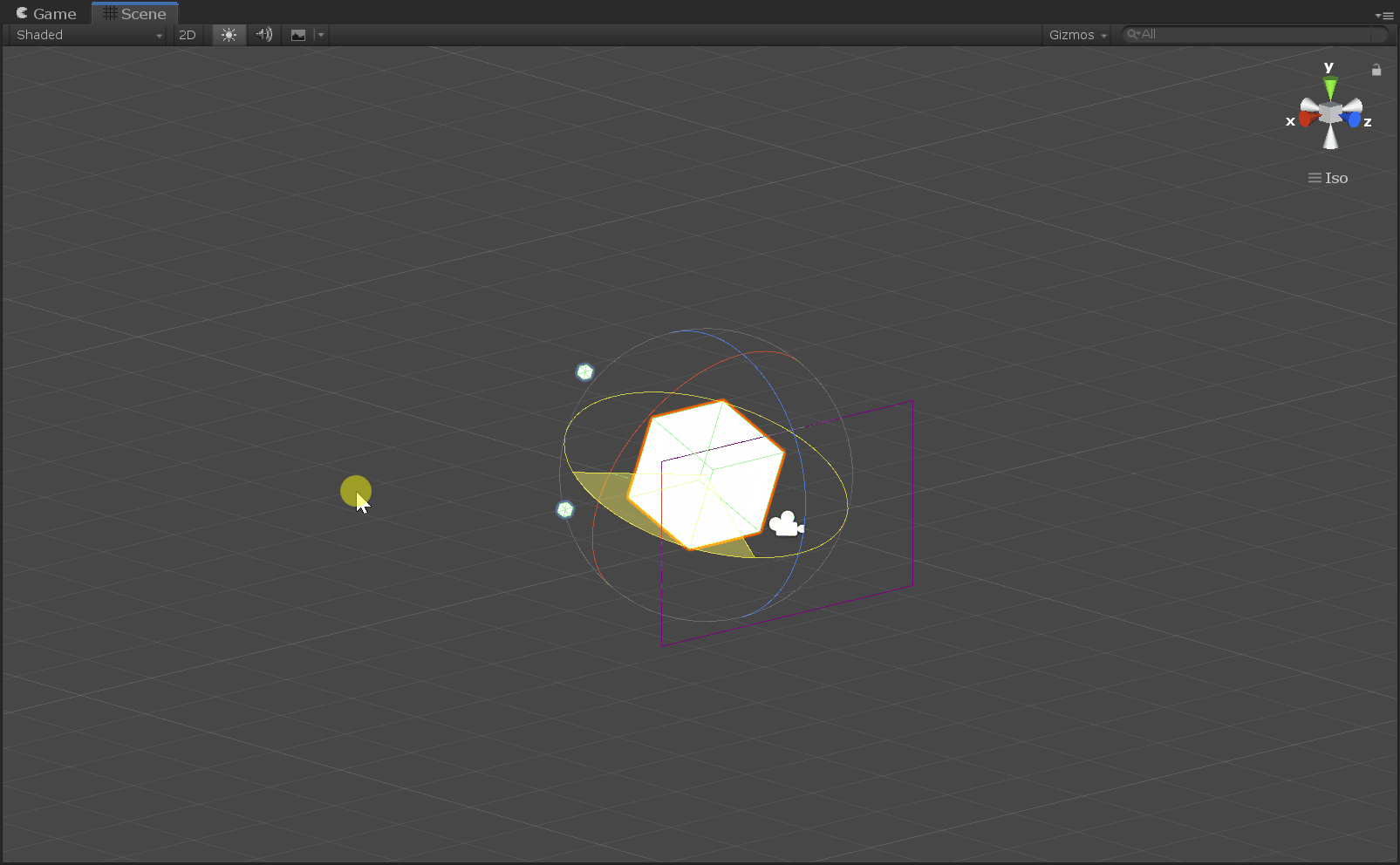
注意:物体自身的坐标轴正方向会随着物体的旋转而改变,而外部轴/世界坐标轴正方向是始终不变的,不随着物体旋转而改变。在连续的旋转变换中,下面给出的旋转矩阵针对的“轴”,要以外部轴/世界坐标轴的方式去理解。
从数学上给出示例进行解释,首先对于x、y、z轴上的旋转,有下述旋转矩阵
\[ \begin{equation}R_x(\theta)=\begin{bmatrix}1&0&0\\0&\cos{\theta}&-\sin{\theta}\\0&sin{\theta}&\cos{\theta}\end{bmatrix}\end{equation} \]
\[ \begin{equation}R_y(\theta)=\begin{bmatrix}\cos{\theta}&0&\sin{\theta}\\0&1&0\\-\sin{\theta}&0&\cos{\theta}\end{bmatrix}\end{equation} \]
\[ \begin{equation}R_z(\theta)=\begin{bmatrix}\cos{\theta}&-sin{\theta}&0\\\sin{\theta}&\cos{\theta}&0\\0&0&1\end{bmatrix}\end{equation} \]
我们固定按照x、y、z轴的顺序进行旋转,并假设沿x轴旋转任意度,沿y轴旋转90°,再沿z轴旋转任意度,可以得到如下结果:沿物体y轴旋转后,物体z轴变换到了原来物体x轴的方向(即同一个世界轴方向)。也就是说三次旋转变换仅仅覆盖了两个外部轴/世界轴的旋转,一个自由度就这样丢失了,这也就导致了Gimbal Lock的现象。
将变换用公式进行理解:
\[ \begin{equation}\begin{aligned}E(\alpha,\frac{\pi}{2},\beta)&=R_z(\beta)R_y(\frac{\pi}{2})R_x(\alpha)\\&=\begin{bmatrix}0&\sin({\alpha-\beta})&\cos({\alpha-\beta})\\0&\cos({\alpha-\beta})&-\sin({\alpha-\beta})\\-1&0&0\\\end{bmatrix}\\&=R_y(\frac{\pi}{2})R_x(\alpha-\beta)\end{aligned}\end{equation} \]
*补充解释在一些旋转描述中可能看到的术语:pitch是俯仰角,围绕x轴转动;yaw是偏航角,围绕y轴转动;roll是翻滚角,围绕z轴转动。起源于航空术语,想象一架飞机,头部指向z轴正方向,左机翼指向x轴正方向,可能会易于理解。